Matematiksel sezgi, çoğu zaman doğruluğundan emin olabileceğimiz fikirlerle yönlendirilir. Ancak bazen bu sezgiler yanıltıcı olabilir. Üç matematikçi, popüler bir olasılık teorisi olan 'bunkbed konjektürünün' yanlış olduğunu kanıtladılar.
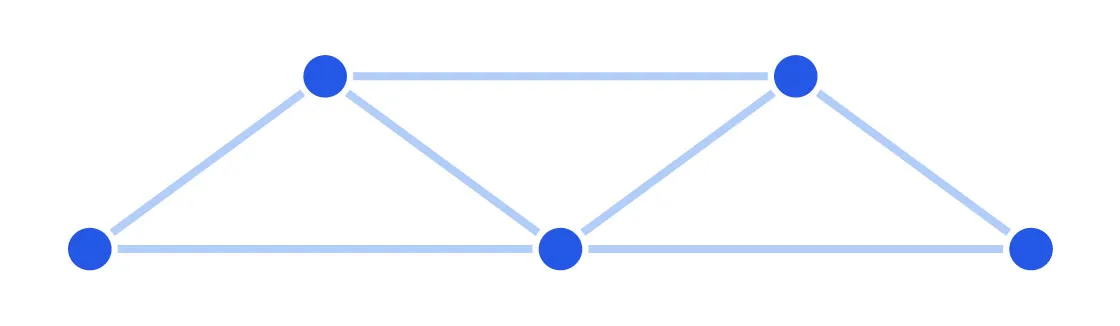
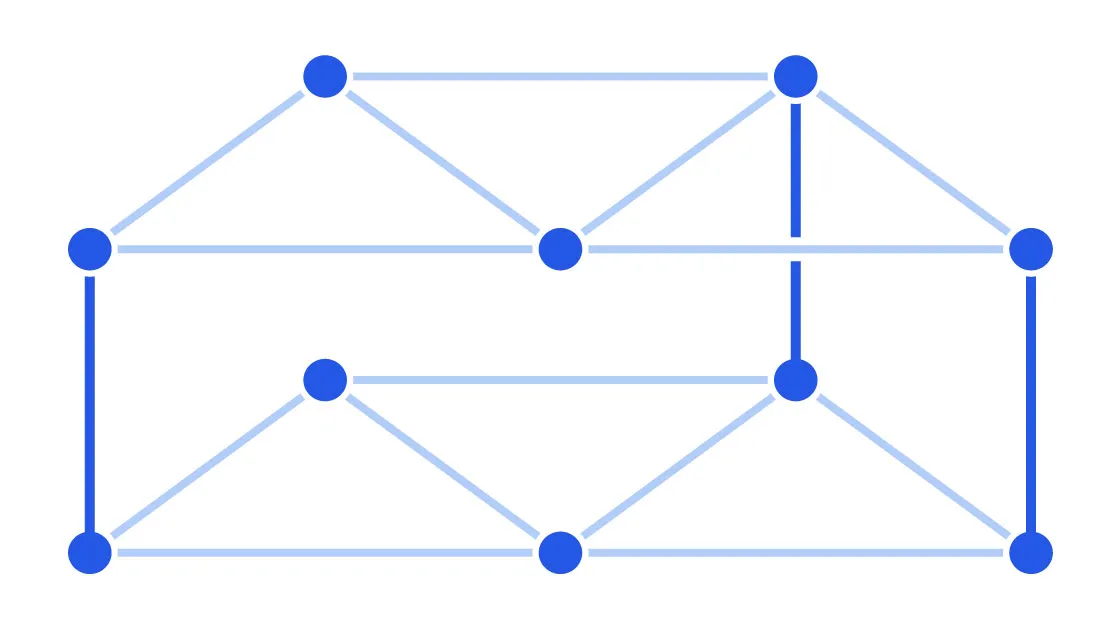
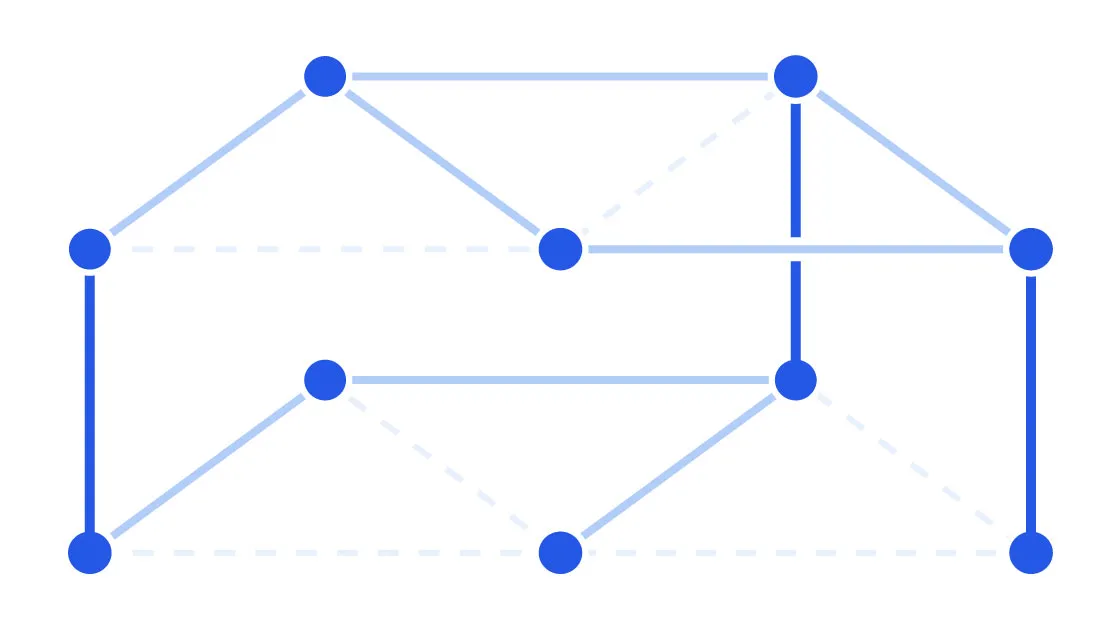
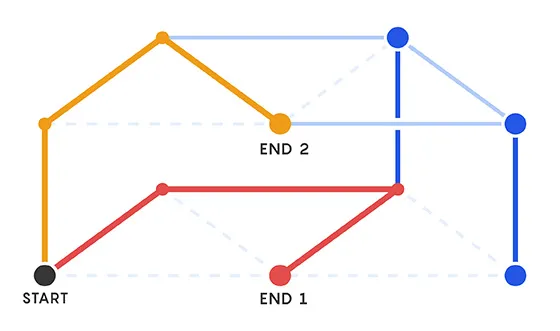
Bunkbed konjektürü, üst üste yığılan matematiksel yapılar arasında dolaşırken, alt katmanlarda yolların bulunma olasılığının her zaman üst katmanlardan daha fazla olduğunu öne sürüyordu. Ancak bu konjektür, matematikçilerin sezgilerinin tersine, yanlış çıktı. Bu yanlışlık, sadece ilgili fiziksel problemlere dair yeni bir bakış açısı getirmekle kalmadı, aynı zamanda matematiksel teorilerin nasıl çalıştığını sorgulatan derin bir ders verdi.
1980'lerde, Hollandalı fizikçi Pieter Kasteleyn, sıvıların gözenekli katılarda nasıl hareket ettiğini matematiksel olarak kanıtlamak için bu konjektürü ortaya koymuştu. Konjektür, üst üste iki grafik yapısının arasındaki geçiş yollarını incelediğinde, alt katmanlardaki yolların daha fazla olacağını savunuyordu. Matematikçiler, bu öneriyi, sıvıların bir malzeme içinde nasıl hareket ettiğine dair önemli bir fiziksel varsayımı doğrulamak için kabul etmişti.
Ancak 2023 yılında, California Üniversitesi'nden Igor Pak ve ekibi, yıllarca süren çalışmaları sonucunda, bu teorinin yanlış olduğunu ortaya koydular. Pak, daha önce bu konjektürün doğruluğundan şüphe ediyordu. Başlangıçta matematikçiler bu sezgiyi doğru kabul etmişlerdi, çünkü alt katmandaki yolların daha fazla olması gerektiği mantıklı bir varsayımdı. Pak, bu tür yanlış inançların matematik dünyasında yaygın olduğunu belirtti ve matematikçilerin daha fazla sorgulama yapmaları gerektiğini savundu.
Pak ve ekibi, konjektürün yanlışlığını ispatlamak için ilk başta, her grafiği tek tek kontrol ettiler. Ancak grafiklerin büyüklüğü arttıkça, her olasılığı incelemek imkansız hale geldi. Bunun üzerine, makine öğrenimi tekniklerinden faydalanarak, farklı grafikler oluşturup bu yapıların üst katmana geçişlerde ne kadar olasılık sunduğunu incelediler. Ancak, yine de her olasılığı tam olarak incelemek mümkün olmadı.
Sonunda, Cambridge Üniversitesi'nden Lawrence Hollom, bu konjektürün farklı bir biçimini çürütmeyi başardı. Hollom'un çalışması, grafikleri değil, hipergrafikleri inceledi ve farklı bir bağlamda, bunkbed konjektürünün yanlış olduğunu gösterdi. Hollom, grafikteki iki nokta arasındaki geçişi değil, birden fazla nokta arasındaki olasılıkları inceledi.
Matematik dünyasında, genellikle bir teoremin doğru olduğunu ispatlamak çok daha yaygın bir yaklaşımken, yanlış olduğunun gösterilmesi daha zor ve az tercih edilen bir yoldur. Pak ve ekibi, uzun süreli başarısız denemelerinin ardından, teorik bir argümanla bu yanlışlığı ortaya koymaya karar verdiler. Konjektürün yanlışlığının ispatlanması, sadece matematiksel teorilerde değil, fiziksel modellerde de devrim niteliğinde bir gelişme sağladı.